In my first graduate macro class, our instructor started with a seemingly basic question: “What are the fundamental building blocks of any economic model?”
Our class struggled to get to an answer. Supply and demand? Not really. Thinking at the margin? Nope. Math? Alas, not.
After generous help from our instructor, we arrived at these bullet points on the blackboard:
Preferences;
Beliefs;
Equilibrium.
We need preferences to model purposeful behavior. We need beliefs to model how agents perceive the world. We need a concept of equilibrium to describe how these agents interact with each other. Any economic model, neoclassical or Keynesian, Marxist or Austrian, mathematical or verbal, must take a stand on these things.
This post is on that second fundamental building block of economic models—beliefs. Or, as beliefs about future outcomes are called in macroeconomics, expectations.
It’s also about two papers that, together with Florian Peters and Artūras Juodis, we finally got published after years of work.
In the beginning, there was FIRE
Expectations play a crucial role in macro:
If people expect inflation to be high next year, they will negotiate for salary increases, pushing up wages and, thereby, inflation;
If investors believe bitcoin will do well in the future, they will buy more bitcoin, driving up its price today;
If bank depositors believe other depositors are withdrawing their money, they will rush to grab their cash first, resulting in a bank run.
In this way, at least in part, many macro variables are determined by the expectations of these macro variables.
But how, exactly, do people form these expectations? For a long time, the working hypothesis was full-information rational expectations (a.k.a. FIRE). The basic assumptions are that people have full information about the economy (FI in FIRE), and their subjective model of the economy coincides with the “true model” of the economy (R in FIRE).
FIRE is an attractive assumption. Models with FIRE are not necessarily easy to solve (they’re not), but they’re tractable. In addition, you don’t need to spend time formulating how people form expectations. “Rational expectations” simply means “model-consistent.” Once you write down the model, expectations come out as a side product, with no extra effort needed.
However, over time, more and more evidence accumulated that expectations violate the key tenets of FIRE. Multiple great surveys of the field go into much depth (here are three: [1]; [2]; [3]).
Here’s a quick sampler of the evidence, though. The graph below depicts average expectations of stock market returns in a sample of individual investors:
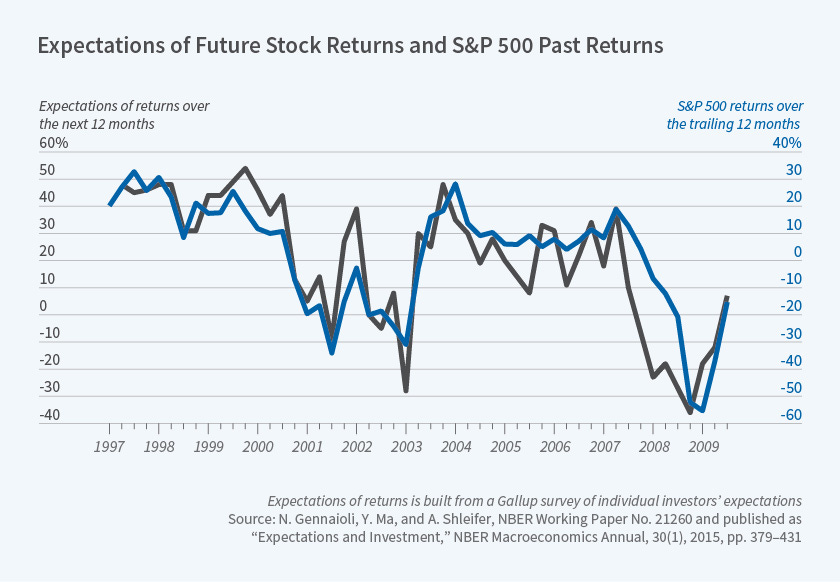
These expectations are extrapolative: Investors expect high returns after a stock-market bull run. However, if anything, realized returns tend to be lower when investors expect great things. That seems very far off from what we would expect from rational expectations.
This graph suggests that investors overreact to past information. They seem to look at a past bull run (which has little predictive power) and extrapolate that the party won’t stop.
So far, so good. Except that there is a whole branch of economics that mostly looks at how expectations underreact to news! For example, in a highly influential paper, Olivier Coibion and Yuriy Gorodnichenko found that inflation expectations respond slowly to macro shocks. That gives rise to predictable forecast errors. For example, the next graph shows how inflation forecast errors respond to a disinflationary technology shock:

And we have all seen “hedgehog graphs” like the one below, plotting inflation in the Euro area vs. predictions from professional forecasters at different points in time:

These professional forecasters are slow to adjust to shocks to inflation, believing in much faster mean reversion than is actually the case.
All in all, we have a puzzle:
Finance evidence suggests that expectations overreact;
Macro evidence suggests that expectations underreact.
What gives?
Part I: Measuring bias
This brings us to 2017.
Back then, Florian Peters and I were both at the University of Amsterdam. Florian was doing research in behavioral finance; I was primarily working on banking theory. However, I attended the Yale Summer School in Behavioral Finance during my Ph.D. studies, and I was very interested in the field. Somehow we got talking about this whole “overreaction, underreaction” puzzle.

One day, Florian shared an exciting working paper by Yueran Ma, Augustin Landier, and David Thesmar.1 Ma, Landier, and Thesmar ran a forecasting experiment in which they asked subjects to predict future outcomes of an AR(1) process. These authors found that expectations had “both extrapolation and underreaction patterns”.2 However, what they meant by “extrapolation” was a type of overreaction. Florian and I were perplexed: How can expectations of the same people, in the same experiment, both under and overreact?
After much head-scratching, we realized that what was happening in the experiment was persistent overreaction. Actually, there was a graph in the original working paper which made it very clear:
After a positive shock to the target variable, x, at time t, subjects overreacted not only at time t but also at t+1, t+2, and so on. So, really, it’s not that expectations had “both extrapolation and underreaction patterns,” as that old abstract stated. No, this was just persistent overreaction.
That got us thinking about expectation formation in terms of impulse-response functions. Isn’t overreaction just what occurs when people perceive the impulse-response function to be bigger than it actually is? Once we had that insight, we realized we could frame all existing models of biased expectation formation as some deviation between perceived and actual impulse-response functions. What’s more, impulse-response functions gave us a way to estimate under and overreaction from data on forecast errors. Maybe we can finally get some clarity on that whole under/overreaction debate!
Funnily enough, we soon realized that our groundbreaking idea was already pre-shadowed by John Muth in his classic 1961 article that introduced rational expectations. Muth considered a special case of our framework in which agents under or overreact to the most recent shock:
Thankfully for us, Muth stopped there, and he also did not provide any way to estimate biases in the data. (That was 20 years ago before Christopher Sims taught us how to estimate VARs, so that’s understandable.)
That was it. Or mostly it. It took us five more years to work out all the wrinkles until the paper finally got accepted for publication in mid-2022. When I now look at the first drafts of the article, I’m surprised by how totally incomprehensible and muddled they were. But the fundamental ideas were already there, in a rough unpolished way, back in late 2017.
Part II: Measuring noise
In 2018 I used to go out on many long runs, mostly in Amsterdam’s beautiful Westerpark:

During one of those long runs, I listened to a “Conversations with Tyler” episode in which Tyler Cowen spoke with Daniel Kahneman. (If you are not a subscriber to CWT, stop reading, and subscribe immediately.)
At some point, they discussed Kahneman’s upcoming book:
COWEN: Much of your last book is about bias, of course. And much of your next book will be about noise. If you think of actual mistakes in human decision-making, how do you now see the relative weight of bias versus noise?
KAHNEMAN: […] it’s hard to say what there is more of, noise or bias. But one thing is very certain — that bias has been overestimated at the expense of noise. Virtually all the literature and a lot of public conversation is about biases. But in fact, noise is, I think, extremely important, very prevalent.
That was a light-bulb moment: All we were doing with Florian was measuring bias. We were completely ignoring noise. Just like the rest of the literature!
Kahneman and co-authors had a nice way of visualizing the difference between noise and bias. For example, imagine that you are trying to predict inflation next quarter. If you are accurate, your forecasts may look like this:

You will never be perfectly on target because unpredictable shocks will always happen.
If you are biased, you are systematically off-target:
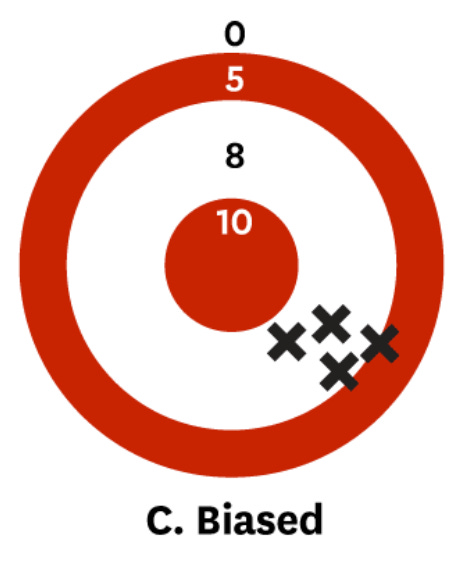
However, if you are noisy, you may be correct “on average” but still all over the place:

These simple graphs illustrate a general point: Noise and bias are equally bad for forecasting accuracy. We cannot ignore noise just because bias is more vibey or whatever. We must understand and measure both.
After returning from my run, I began thinking about measuring noise in expectations. I had an idea: Let's estimate two models, one with individual and one with average expectations. The model using individual expectations should be much more sensitive to noise. Perhaps we can use the difference in estimates to calculate noise?3
For instance, suppose we estimate a Mincer-Zarnowitz regression at the level of average expectations:
Next, we perform the same calculation but with individual forecasters:
If individual forecasts are noisy, we will see a smaller β in the second regression due to something called attenuation bias.
The second regression, however, is a panel-data regression, and I was unsure how to calculate its attenuation bias. So, I started talking with Artūras Juodis, a fantastic panel-data econometrician who knows everything about this kind of stuff.
Long story short, the initial idea did not work (most initial ideas don’t work). The reason is that you need a lot of assumptions to back out the level of noise from the difference in β’s. Thankfully, Artūras had a better idea. How about we run a factor model on individual expectations, eliminate the factor component, and recover noise?
That was a brilliantly simple idea. What’s more, because of our previous work with Florian, we knew that essentially all models of expectation formation satisfy a factor structure. That means we could use this factor-model approach without making any strong assumptions.
Again, it took us quite some time to work out all the details. Once we had a good draft, we shared the article with Daniel Kahneman. Naturally, we were not expecting any response. However, not even half an hour after hitting “send,” we received the kindest and most encouraging reply from the Nobel-prize laureate.
That was one of my academic career's sweetest and most encouraging moments.
Taking stock
OK, so here’s the story so far:
Expectations are a fundamental building block of economic models;
There is much confusion on whether expectations under or overreact;
We wrote some papers on how to measure bias & noise in expectations;
Daniel Kahneman is the kindest person ever.
So, what did Florian, Artūras, and I discover? Do expectations under or overreact? Here’s a quick summary:
Expectations, even those of professional forecasters, contain a lot of noise. That means there’s a lot of “overreaction” to idiosyncratic noise;
Forecasters underreact to aggregate shocks (such as interest rate changes) for inflation expectations. It’s not that inflation expectations “overreact at the individual level” but “underreact at the consensus level.” Instead, forecasters react differently to various kinds of information: Overreaction to noise, underreaction to aggregate shocks.
However, the most significant contribution of our work is in the methods we developed. Our two papers offer a reliable way to measure bias and noise. Honestly, there’s a lot of confusion in this field about measuring under and overreaction, and many commonly used methods aren’t effective. Noise is often ignored altogether. We can and should do better, and these two papers provide practical solutions on how to do that.
So, if you are interested in expectations, I’d recommend taking a look:
Measuring Under- and Overreaction in Expectation Formation (with Florian Peters, forthcoming in Review of Economics and Statistics);
Quantifying Noise in Survey Expectations (with Artūras Juodis, forthcoming in Quantitative Economics).
As I finish writing this post, I’m painfully aware that the task of understanding expectation formation is far from over. The methods we developed are not without issues and can certainly be improved. It’s a long run, but I’m sure we will continue learning about that critical fundamental building block of economic models.
This paper recently got published in a much revised and updated form—together with Hassan Afrouzi and Spencer Kwon—in the Quarterly Journal of Economics.
See the abstract of the 2017 working paper version.
The idea was inspired by a paper that Pedro Bordalo, Nicola Gennaioli, Yueran Ma, and Andrei Shleifer released on “Over-Reaction in Macroeconomic Expectations in the summer of 2018.


