Why no one agrees on p(doom)

Reference class problem coupled with weak evidence makes for radical uncertainty

Source: ChatGPT

How dangerous is advanced artificial intelligence?

Ask ten AI experts, and you’ll probably get ten different answers. Take Yann LeCun and Geoff Hinton, two AI pioneers who—together with Yoshua Bengio—shared the Turing Award in 2018.

LeCun (Chief AI Scientist at Meta) believes that the probability of AI causing human extinction is very small, less than the chance of an asteroid hitting the Earth. Hinton (winner of the 2024 Nobel Prize in Physics) is around 50:50. That’s a massive disagreement over one of the most consequential questions faced by humanity.

This probability of AI causing human extinction is often cheekily called p(doom), and estimates vary wildly. Here are some examples:

How can reasonable people disagree so much?

I’ll argue that these disagreements have two root causes:

• Reference class problem: Depending on the reference class you pick (i.e., is AI similar to past human tech, or is AI to humans as Homo sapiens was to Neanderthals?), you’ll come up with wildly different base rates;

• Weak evidence: Current evidence for updating base rates (e.g., recent AI progress; advances in safety research; regulatory momentum) is weak and shouldn’t update you too much.

The striking implication is that p(doom) mostly depends on which analogy for AI you find most compelling. What’s worse: We don’t have a principled way to choose among the available analogies.

This radical uncertainty is frustrating, but it’s also clarifying. We should be explicit about which analogies drive our views. We can use different analogies to set bounds—maybe AI risk is somewhere between “new powerful tech” (lower risk) and “new dominant species” (higher risk). Most importantly, even if we can’t pin down the exact probability, we can agree that any non-trivial chance of extinction deserves serious attention.

In this post, I’ll develop a Bayesian model to quantify this intuition, showing how different reference classes lead to p(doom) estimates ranging from <0.1% to >80%. The key result is given below, depicting base rates and updated beliefs for some plausible reference classes. (The code generating all the results in this post is here.)

1. Reference class problem

In theory, estimating p(doom) should be straightforward:

1. Define the relevant reference class;

2. Use data from the reference class to calculate your prior (a.k.a. base rate);

3. Update your prior with new evidence following the Bayes’ rule.

A key reason why estimating p(doom) is so difficult is step 1.

First, no technology has ever caused human extinction.¹ As a result, we can’t calculate base rates in the usual way. This forces us to rely on analogies—which are by definition imperfect. We’re looking for situations that share some important features with “AI causes human extinction” but aren’t actually that thing.

It gets worse because there are multiple reasonable analogies to choose from. For example, you could compare AI to nuclear weapons. While nuclear weapons are risky, we have survived 80 years with them, so maybe we’ll survive AI, too. On the other hand, you could compare humans creating AGI to a Neanderthal inviting Homo sapiens to sit by the campfire. It seems like that wouldn’t have worked out well for the Neanderthal, and possibly won’t for humans with AGI either.

2. Different classes, different base rates

The simplest “solution” to the reference class problem is to pick your favorite and run with it. In effect, that puts a probability of 1 on your favorite class being correct. However, this seems overconfident given how little we know about AI.

A better approach is to be explicit about the potential reference classes:

• List all potential reference classes;

• Calculate a prior using each class;

• Use the different reference classes to update and get a range of values.

Let’s see how that might look like for p(doom).

Following a high-quality study by the Forecasting Research Institute, I’ll define p(doom) more formally as the probability that AI causes human extinction or reduces the global human population below 5,000 people by 2100.²

I consider four main reference classes, ordered from most to least optimistic. These guesstimations are highly uncertain. However, they do illustrate the range of plausible values:

3. Current AI evidence is weak

To update our base rates, we next need to examine the available evidence and determine its strength.

3.A. Available evidence

Here are the key pieces of evidence I’ll consider:

• Faster-than-expected capabilities progress with progress on benchmarks consistently underestimated;

• No major AI catastrophe so far despite widespread use and deployment (for example, ChatGPT has 400+ million weekly active users and $10 billion in annual recurring revenue);

• Emerging evidence of misaligned AI behavior including in-context scheming, blackmail, and shutdown resistance;

• Advances in AI safety research (for example, mechanistic interpretability); LLM-based AI systems may be more likely to share human values;

• Governance momentum with mixed regulatory signals: Executive order on AI by President Biden signed in 2023 (later rescinded by President Trump); EU AI Act entering into force in 2024.

While not exhaustive, this list captures the key high-level evidence categories.

3.B. How strong is this evidence?

How much should this evidence shift our beliefs? In Bayesian terms, the answer depends on the Bayes factors. My assessment: These factors are close to 1 (weak evidence), for two reasons.

First, consider the baseline. Even moderate-quality scientific studies only achieve Bayes factors within [0.75, 2.00], as I’ve estimated in a previous post. These studies have hundreds to thousands of data points, credible empirical designs, and careful statistical modeling. The current evidence on AI is much more speculative and indirect.

Second, we can calibrate using conditional forecasts. In a separate study, the Forecasting Research Institute asked AI experts how their p(doom) estimates would change given specific “warning shots”:

Source: Forecasting Research Institute

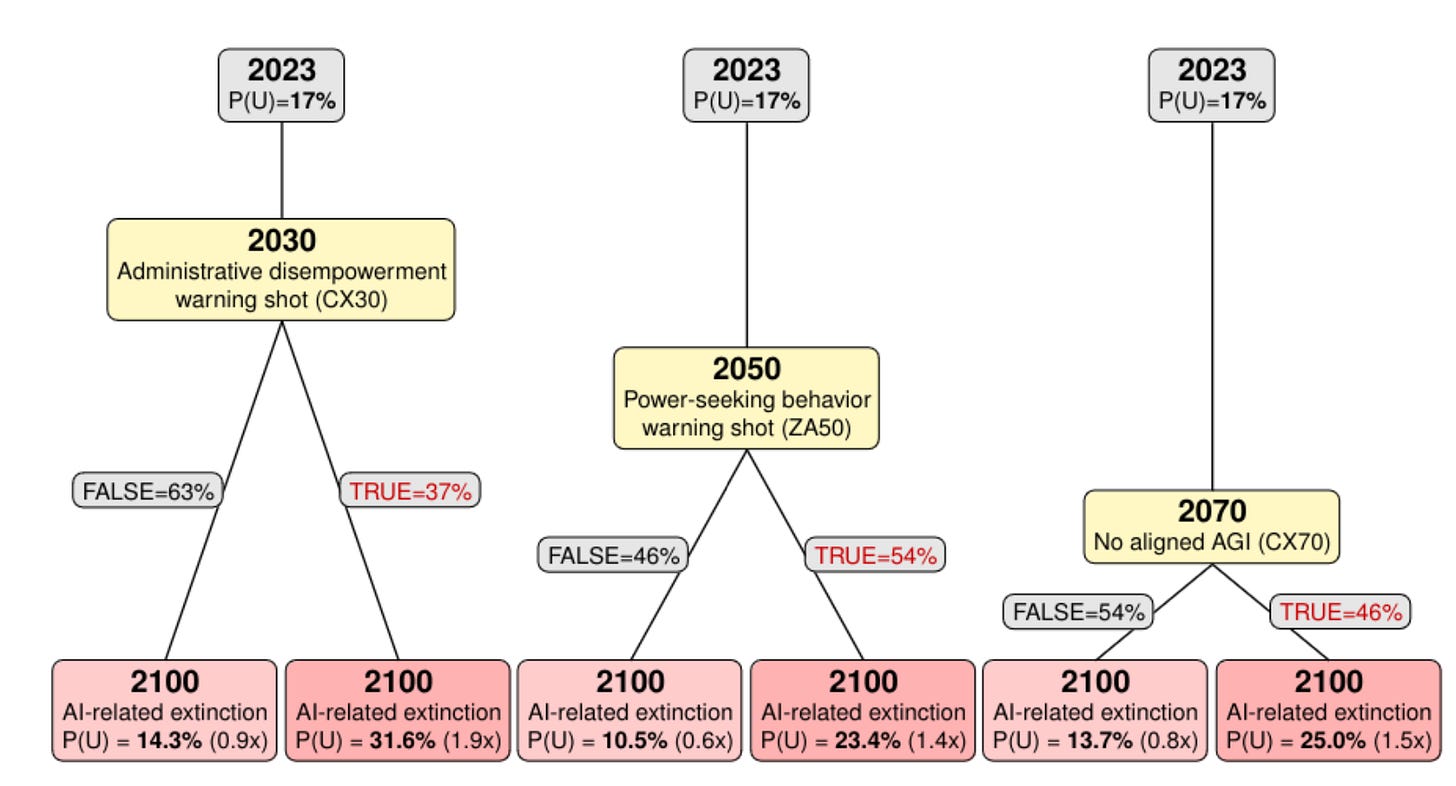
These conditional forecasts reveal the implied Bayes factors:

• An “administrative disempowerment warning shot” (e.g., AI freezing assets or blocking voting) would shift expert p(doom) from 17% to 31.6%.³ That implies a Bayes factor of 2.3 (no warning shot: 0.8);⁴

• A “power-seeking behavior warning shot”⁵ has an implied Bayes factor of 1.5 (no warning shot: 0.6).

Nothing we’ve seen so far approaches these warning shots in severity. This bounds Bayes factors to [0.8, 1.5] for current evidence.

3.C. Estimating specific Bayes factors

To assign factors to each piece of evidence, I subjectively estimate their “relative strength” (compared to the warning shots above) and then scale proportionally:

• 0% relative strength → Bayes factor of 0.8 (for negative evidence) or 1.0 (for positive evidence);

• 100% relative strength → Bayes factor of 1.0 (negative) or 1.5 (positive);

• 50% relative strength → Bayes factor of 0.9 (negative) or 1.25 (positive).

This yields the following estimates:⁶

All Bayes factors cluster near 1.0 (ranging 0.95–1.17). Current evidence provides only weak updates to our base rates in either direction. If we assume that the evidence is independent (not true, but a reasonable benchmark) and multiply the factors, we obtain a joint factor of 1.25. That’s a modest update for p(doom).

4. Putting it all together

We can now combine all the previous ingredients to estimate p(doom):

This calculation takes the base rates from Section 2 and updates them using the Bayes factors of Section 3 (assuming independence).

Here are the key takeaways:

• Updates are modest across all reference classes. The largest shift is just 4.8 percentage points (asymmetric conflicts). Most updates are 2–3 percentage points or less;

• The massive uncertainty persists. Updated estimates still range from 0.03% (human survival record) to 88.2% (human evolution), a factor of nearly 3,000x;

• Disagreements stem from reference classes. Whether you’re optimistic or pessimistic about AI risk depends almost entirely on which historical analogy you find most compelling. The evidence itself is too weak to override these priors.

5. Conclusions

You may have seen this meme:

In the context of p(doom), there are two ways to interpret it.

You could mock people who believe p(doom) discussions are “silly sci-fi speculation.” But you could also read the meme differently. Maybe we don’t actually know what’s “normal” or “weird” when it comes to AI risk. Perhaps anyone claiming high confidence about p(doom) needs a dose of epistemic humility.

In a recent Unherd piece, Tom Chivers offers a perfect historical parallel. In the 1930s, leading experts disagreed on whether nuclear weapons were even possible. Ernest Rutherford, sometimes called the “father of nuclear physics,” declared that “anyone who expects a source of power from the transformation of these atoms is talking moonshine.” He was spectacularly wrong.

Will Yann LeCun end up like Rutherford? Or will we look back at LessWrong posts as exercises in “silly sci-fi speculation”?

I don’t know. I developed this Bayesian model hoping to bring clarity to AI risk debates. Instead, I ended up with estimates ranging from 0.03% to 89%—an almost 3,000x spread!

That does not mean that AI risk is nothing to be worried about. When experts disagree by >100x, the right response isn’t “Oh, I guess nothing to worry about then!” The correct conclusion is to take sensible precautions—like requiring safety evaluations before deploying frontier AI systems—while working to reduce the uncertainty.

While we’re at it, how about another meme?

---

1. Also, by definition, if any such technology had existed, we wouldn’t be here to discuss it.

2. Many people would also include permanent disempowerment of humanity in “doom” (e.g., scenarios as those in the Matrix), which is excluded in the definition.

3. Defined as an event in which an AI system does at least one of the following: “[…] freeze assets affecting ≥1% of the population or ≥0.5% of GDP for over a year; prevent ≥5% of voting-age citizens from participating in a national election; restrict >3% of residents' movement for 3+ months; limit >10% of the population's internet access for 3+ months; or legally restrict >5% of citizens' access to certain housing or employment for 1+ year.”

4. Since (posterior odds) = (prior odds) x (Bayes factor), the Bayes factor can be backed out as (posterior odds) / (prior odds).

5. Defined as an event in which “AI developers must attempt to disable or destroy an AI (costing >$5M) after it exhibits power-seeking behaviors such as acquiring significant resources, controlling financial accounts, manipulating humans, infiltrating key systems, seizing control of weaponry, self-propagation, or engaging in hacking.”

6. If you wish to assign different relative strengths, feel free to experiment with the code in the Colab notebook.